Théorie constructale La petite histoire Comprendre simplement Domaines de présence Son interprétation dans l'avenir Les références Mais encore …

by Pepe ©   Accueil  Arborescence  Page précédente

La petite histoire  Up Page Clé des formes parfaites Trouver la forme idéale d'un système afin qu'il offre un rendement optimal: ce rêve d'ingénieur, la théorie d'un chercheur américain promet d'en faire aujourd'hui une réalité.   Adrian Bejan Né en Roumanie en 1948 et émigré aux Etats-Unis à l'âge de 19 ans, Adrian Bejan est diplômé du prestigieux Masachussetts Institute of Technology (MIT), professeur d'ingénierie mécanique à l'université Duke de Californie du Nord, titulaire de nombreuses médailles scientifiques et docteur honoris causa de onze universités de part le monde, dont celle de Nancy, où l'on n'hésite pas à le présenter comme un "leader scientifique mondial des domaines de l'énergétique-thermique et de la mécanique des fluides". De quoi donner du crédit à sa théorie constructale.

Comprendre simplement  Up Page Dégradation d'énergie Que ce soit de la chaleur, de l'électricité, de l'eau ou n'importe quel flux qui s'écoule dans ses circuits, un système est nécessairement confronté à des résistances, des frottements, des diffusions qui détournent l'énergie vers des lieux où elle devient inexploitable. Les thermodynamiciens ont même fait depuis longtemps de cette inexploitable dégradation d'énergie un principe, avec la notion d'entropie.   Répartir l'imperfection Tout ingénieur sait qu'il est impossible de baisser la température de façon parfaitement homogène. Adrian Bejan propose de se concentrer exclusivement sur les inévitables résistances du système: "Puisque nous sommes condamnés à l'imperfection", résume-t-il, "le seule chose à faire est de la répartir au mieux, via la géométrie". Les équations qui régissent ces processus dégradants sont en effet connues depuis longtemps: dans le cas d'un circuit de refroidissement, la théorie des échanges de chaleur a été formalisée par Joseph Fourier il y a presque deux cents ans. Donc, si l'ingénieur définit clairement la liste des contraintes de son système (caractéristiques des matériaux employés, taille de la surface à refroidir, quantité de chaleur produite, température maximale en chaque point, etc.), ainsi que ses objectifs (minimiser la température la plus haute), rien ne l'empêche d'étudier en détail comment varient ces résistances selon la façon dont les matériaux sont répartis. Le but est de trouver la forme qui en minimise l'ampleur globale.   Simplifier le problème Déterminer la forme élémentaire 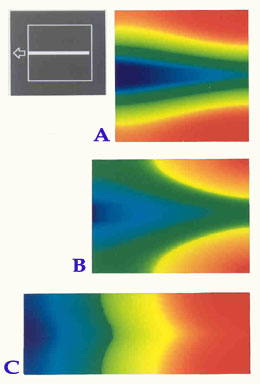La méthode consistera à rechercher d'abord la forme optimale du plus petit volume élémentaire disponible, puis en assembler plusieurs en un volume plus grand, jusqu'à faire émerger la forme globale, en remontant une à une toutes les échelles de grandeur. Dans notre cas précis du circuit de refroidissement, l'ingénieur constructal commence par étudier la géométrie de la plus petite surface rectangulaire à travers laquelle un collecteur de chaleur peut être mis en place, étant données les contraintes pratiques de construction. Equation de Fourier à l'appui, il peut alors déduire le juste milieu, dont les proportions répartissent au mieux la température: si H est la hauteur du rectangle et L sa largeur, la proportion optimale du rectangle est: (H/L)opt=2(kµ)-1/2, où k et µ sotn des constantes, l'une définie par les conductivités des deux matériaux, et l'autre par leurs aires respectives. L'illustration des trois surfaces (A, B et C), montre que la forme optimale sera celle qui présentera une zone rouge (forte déperdition de chaleur) la plus faible. Le proposition B sera donc choisie, car elle minimise ces points chauds.   En assembler plusieurs 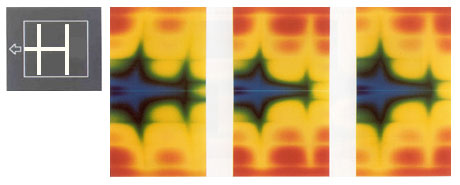Il faut ensuite passer à l'échelle supérieure en réunissant plusieurs de ces surfaces élémentaires "B" en un réseau qui évacue la chaleur vers un seul point. Cet assemblage est lui aussi optimisé à partir des équations afin de minimiser les points chauds.   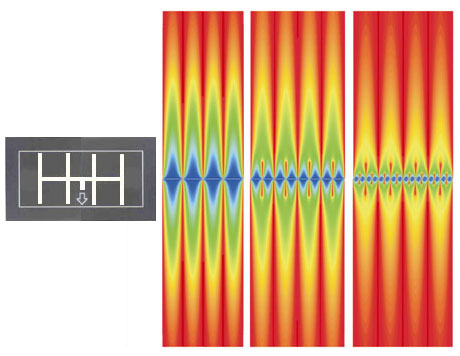Il s'agira donc de répartir au mieux le refroidissement à cette échelle, sans altérer l'optimisation de l'étage inférieur.   Ainsi de proche en proche, et en augmentant progressivement les échelles jusqu'à la taille requise, l'ingénieur constructal fait émerger un réseau de refroidissement au rendement maximal, une arborescence idéale qui répartit au mieux les résistances.   Un dessin parfait car ... le moins imparfait possible !     Faire émerger la forme globale Cette nouvelle méthode commence tout juste à se diffuser dans la communauté des ingénieurs, en particulier aux Etats-Unis, mais aussi en France, où une dizaine de chercheurs y travaillent activement. "Elle est très accessible aux ingénieurs", assure Jocelyn Bonjour, du Laboratoire du froid du Conservatoire national de arts et métiers (CNAM) de Paris, qui l'a découverte il y a deux ans. Elle exploite des équations très classiques et ne nécessite pas, dans la plupart des cas, de gros calculs. La principale difficulté est de se familiariser avec ce nouvel d'esprit. Mais elle a déjà changé ma façon de voir mon métier". Pour Daniel Tondeur, du Laboratoire des sciences du génie chimique du CNRS, à Nancy, "la démarche constructale est encore dans sa préhistoire, mais c'est exactement l'outil dont les ingénieurs avaient besoin".

Domaines de présence  Up Page D'innombrables applications Sylvie Lorente, du département d'ingénierie civile de l'Institut national des sciences appliquées de Toulouse, qui travaille depuis plus de deux ans sur cette théorie, en est une des meilleures spécialistes en France. Elle l'a, par exemple, exploitée pour les réseaux de distribution du chauffage urbain dans le but de minimiser les frottements et les pertes de chaleur. Au bout de ses calculs constructaux, la longueur et l'épaisseur des conduites, le nombre d'embranchements, le rapport de diamètre entre les divers tuyaux, l'angle des connexions ... toutes les caractéristiques du réseau ont été déduites de la seule volonté de chasser au mieux le gaspillage. "Un haut degré de complexité est souvent nécessaire pour optimiser les systèmes, souligne-t-elle, et il est difficile de la gérer sans la théorie constructale".

Son interprétation dans l'avenir  Up Page Rencontre avec Ilya Prigogine "Professeur d'ingénierie spécialiste de thermodynamique, j'ai toujours été intéressé par la géométrie et l'architecture, dans la grande tradition européenne des ingénieurs comme Gustave Eiffel et l'Ecole polytechnique Il y a dix ans, j'ai commencé à travailler sur un système de refroidissement du boîtier électronique des ordinateurs. Or, plus j'optimisais ce système, plus la forme des réseaux de courants internes ressemblait à celle d'un arbre, avec des ramifications de plus en plus intriquées de plus en plus fines. Le déclic survint en 1995 à Nancy, lors d'une conférence du prix Nobel de chimie Ilya Prigogine qui affirmait que les structures en formes d'arbres ne sont pas des structures déterministes mais sont caractéristiques d'un processus aléatoire. J'ai tout de suite pensé que cela était faux: j'avais montré qu'une telle géométrie résulte, au contraire, d'un principe d'optimisation, qu'elle est nécessaire pour miminiser la thermorésistance et assurer le contact le plus intime possible entre le chaud et le froid. J'ai été alors convaincu que tout un pan de l'analyse géométrique en ingénierie était à repenser. Sans la chance d'entendre ce grand homme, je serais resté ingénieur. Aujourd'hui, mon travail est beaucoup plus général". Adrian Bejan, professeur d'ingénierie mécanique à l'université Duke de Californie du Nord.   Origine du mot "constructal" "Je l'ai choisi en écho au mot "fractal", élaboré par Benoît Mandelbrot à partir du verbe latin frangere ("briser") pour décrire ces nouvelles formes géométriques, dont le motif, de plus en plus petit, se répète à l'infini. Ce mot fractal suggère, selon moi, une mauvaise direction: les choses ne se fragmentent pas, mais s'agrègent, se construisent, du petit vers le grand. J'ai donc baptisé ma théorie à partir du verbe latin construere, devenu "construire" en français et roumain et "construir" en espagnol et portugais. Selon moi, notre monde n'est pas fractal, il est constructal." Adrian Bejan, professeur d'ingénierie mécanique à l'université Duke de Californie du Nord.

Les références  Up Page Réseau Pepe Science et Vie   Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les "trois pôles d'intérêts", en psychologie)_ c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous.   Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil).

Mais encore …  Up Page Géométrie optimale Tous les systèmes énergétiques, vivants ou inertes, semblent obéir à une géométrie optimale, façonnée au fil du temps. "Pour qu'un système naturel persiste dans le temps", résume Adrian Bejan, il doit évoluer de telle manière qu'il fournisse un accès plus facile aux flux imposés qui les traversent".   Réexaminer la nature Si l'ingénieur et le biologiste décrivent tous deux comment fonctionnent les systèmes naturels, l'ingénieur, lui, décrit comment augmenter leur performance. Et s'il suit le principe constructal, il est alors en mesure de prédire les formes que la Nature tend à sculpter avec le temps, en déduisant par un raisonnement physique le chemin qu'elle a parcouru par tâtonnement. Poumons humains, plumes d'oiseau ou craquelures du sol, toutes les structures vivantes ou inertes peuvent donc être désormais réexaminer avec les lunettes de l'ingénieur, en les considérant comme des systèmes énergétiques soumis tout à la fois à des flux, des contraintes et des objectifs.   Un vrai virage théorique La forme globale d'un système naturel est rarement déterminée a priori, mais émerge d'une multiplicité d'interactions, de la plus petite vers la plus grande échelle."La forme globale de l'os émerge de la somme d'optimisations locales", explique, par exemple, André Dittmar, de l'Institut national des sciences appliquées de Lyon. Des capteurs mesurent en permanence la pression sur l'os et obligent à mettre de la matière là où elle est la plus forte. La géométrie fractale, dont les arborescences infinies étaient censées décrire ces formes naturelles, a eu l'immense mérite de focaliser sur cette notion d'échelle. Mais, pour décrire le processus morphologique naturel, la dynamique fractale va dans la mauvaise direction: ce n'est pas par fragmentation que les formes s'engendrent, mais par construction et optimisation. La théorie constructale, qui organise les échelles dans l'espace, de la plus petite vers la plus grande, est, en ce sens, beaucoup plus "naturelle". De plus, alors que la géométrie fractale est descriptive (avec un algorithme postulé dès le départ), immatérielle (aves des branches infiniment petites) et particulières (avec un même dessin qui se répète à chaque échelle), la théorie constructale, elle, est prédictive (avec un seul et unique principe d'optimisation d'où tout découle), réaliste (avec une taille finie prédite pour la plus petite brindille) et très générale ( avec une organisation spécifique à chaque échelle selon les lois physiques en jeu). Heitor Reis était plutôt sceptique lorsqu'Adrian Bejan lui a proposé, d'exploiter la théorie constructale pour étudier le plus gros système à écoulement de la Terre: l'atmosphère. "J'ai été très surpris de la précision des résultats", reconnaît ce spécialiste de géophysique de l'université d'Evora, au Portugal. A partir du moment où l'on considère bles transferts de chaleur dans l'atmosphère optimisés, la théorie constructale prédit en effet une partition en différents ciels suivant des latitudes très proches de ce que l'on a observé jusqu'ici de façon empirique. Même chose pour la température ou l'altitude des vents".   Processus d'auto-organisation Dans ses fascinants travaux, "Forme et croissance", publiés en 1917, d'Arcy Wentworth Thompson multiplie les comparaisons entre créatures naturelles (en montrant par exemple comment tordre la silhouette d'un poisson pour obtenir celle d'un autre), ainsi que les similitudes avec les phénomènes physiques et les oeuvres des ingénieurs (en comparant les formes des méduses et des gouttes de paraffine dans l'eau, ou des squelettes de bison et des ponts suspendus). On observe le monde avec les yeux d'un géomètre, les formes naturelles lui apparaissent alors comme le résultat des contraintes issues de l'action des forces physiques. En 1952, le chercheur britannique Alan Turing a montré comment des réactions entre processus chimiques engendrent des taches caractéristiques es pelages de nombreux animaux, et peuvent même être à la base d'appendices corporels, comme les doigts des animaux ou les branches des végétaux. Une forme complexe pourrait donc émerger de l'action de processus très élémentaires ... Cette vision dynamique de la morphologie est aujourd'hui prise très au sérieux Pour Vincent Fleury, du Laboratoire de physique de la matière condensée, à l'Ecole polytechnique, auteur d'un ouvrage sur le sujet, "même si le mécanisme de Turing ne joue probablement aucun rôle dans la genèse des formes de la nature, les notions fondamentales sont bien, selon moi, les processus de ruptures de symérie et d'organisation." L'équipe d'Yves Couder de l'Ecole normale supérieure de Paris a d'ailleurs récemment montré comment la forme des veines des feuilles n'est pas déterminée a priori mais est le résultat d'un jeu complexe entre forces mécaniques.   Sadi Carnot, le précurseur Avec sa vision géométrique, évolutionniste, auto-organisatrice et multi-échelle, la théorie constructale s'inscrit dans cette longue quête. Mais si son principe plonge dans les idées d'Euclide, d'Aristote, de Darwin, de d'Arcy Thompson, de Mandelbrot, voire de Wolfram, c'est en fait avec Sadi Carnot qu'Adrian Bejan se reconnaît une véritable filiation. Grâce aux Réflexions sur la puissance du feu et sur les machines propres à développer cette puissance que ce polytechnicien français de 26 ans a publiées en 1824, les ingénieurs savent que le rendement des machines est limité par l'irréversible dégradation d'énergie. Ils savent que la forme prafaite n'est pas naturelle. Ou plutôt, que la perfection ne s'atteint en ce bas monde matériel qu'en optimisant ses inévitables imperfections.